Problem Statement

There is a railroad in Takahashi Kingdom. The railroad consists of N sections, numbered 1, 2, ..., N, and N+1 stations, numbered 0, 1, ..., N. Section i directly connects the stations i-1 and i. A train takes exactly A_i minutes to run through section i, regardless of direction. Each of the N sections is either single-tracked over the whole length, or double-tracked over the whole length. If B_i = 1, section i is single-tracked; if B_i = 2, section i is double-tracked. Two trains running in opposite directions can cross each other on a double-tracked section, but not on a single-tracked section. Trains can also cross each other at a station.

Snuke is creating the timetable for this railroad. In this timetable, the trains on the railroad run every K minutes, as shown in the following figure. Here, bold lines represent the positions of trains running on the railroad. (See Sample 1 for clarification.)

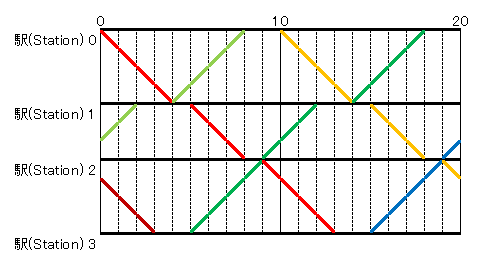
When creating such a timetable, find the minimum sum of the amount of time required for a train to depart station 0 and reach station N, and the amount of time required for a train to depart station N and reach station 0. It can be proved that, if there exists a timetable satisfying the conditions in this problem, this minimum sum is always an integer.

Formally, the times at which trains arrive and depart must satisfy the following:

• Each train either departs station 0 and is bound for station N, or departs station N and is bound for station 0.
• Each train takes exactly A_i minutes to run through section i. For example, if a train bound for station N departs station i-1 at time t, the train arrives at station i exactly at time t+A_i.
• Assume that a train bound for station N arrives at a station at time s, and departs the station at time t. Then, the next train bound for station N arrives at the station at time s+K, and departs the station at time t+K. Additionally, the previous train bound for station N arrives at the station at time s-K, and departs the station at time t-K. This must also be true for trains bound for station 0.
• Trains running in opposite directions must not be running on the same single-tracked section (except the stations at both ends) at the same time.

Constraints

• 1 \leq N \leq 100000
• 1 \leq K \leq 10^9
• 1 \leq A_i \leq 10^9
• A_i is an integer.
• B_i is either 1 or 2.

Partial Score

• In the test set worth 500 points, all the sections are single-tracked. That is, B_i = 1.
• In the test set worth another 500 points, N \leq 200.

Sample Input 1

3 10
4 1
3 1
4 1

Sample Output 1

26

For example, the sum of the amount of time in question will be 26 minutes in the following timetable:

In this timetable, the train represented by the red line departs station 0 at time 0, arrives at station 1 at time 4, departs station 1 at time 5, arrives at station 2 at time 8, and so on.

Sample Input 2

1 10
10 1

Sample Output 2

-1

Sample Input 3

6 4
1 1
1 1
1 1
1 1
1 1
1 1

Sample Output 3

12

Sample Input 4

20 987654321
129662684 2
162021979 1
458437539 1
319670097 2
202863355 1
112218745 1
348732033 1
323036578 1
382398703 1
55854389 1
283445191 1
151300613 1
693338042 2
191178308 2
386707193 1
204580036 1
335134457 1
122253639 1
824646518 2
902554792 2

Sample Output 4

14829091348