Max Score: $800$ Points
E869120 the coder moves in the graph as follows:
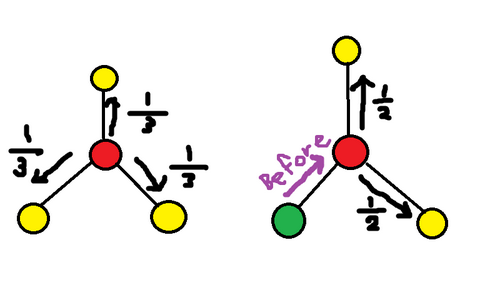 Calculate the expected value of the number of turns, when E869120 starts from vertex i, for all i (1 ≤ i ≤ N).
Calculate the expected value of the number of turns, when E869120 starts from vertex i, for all i (1 ≤ i ≤ N).
Problem Statement
There is an undirected connected graph with $N$ vertices and $N-1$ edges. The i-th edge connects u_i and v_i.E869120 the coder moves in the graph as follows:
- He move to adjacent vertex, but he can't a visit vertex two or more times.
- He ends move when there is no way to move.
- Otherwise, he moves randomly. (equal probability) If he has $p$ way to move this turn, he choose each vertex with $1/p$ probability.

Input
The input is given from standard input in the following format.
N
u_1 v_1
u_2 v_2
:
u_{N-1} v_{N-1}
Output
In i-th (1 ≤ i ≤ N) line, print the expected vaule of the number of turns E869120 moves.The relative error or absolute error of output should be within 10^{-6}.
Constraints
- $1 \le N \le 150,000$
- The graph is connected.
Subtasks
Subtask 1 [ $190$ points ]
- There is no vertex which degree is more than 2.
- This means the graph looks like a list.
Subtask 2 [ $220$ points ]
- 1 ≤ N ≤ 1000.
Subtask 3 [ $390$ points ]
- There are no additional constraints.
Sample Input 1
4 1 2 2 3 2 4
Sample Output 1
2.0 1.0 2.0 2.0
Sample Input 2
4 1 2 2 4 4 3