Problem Statement

A balancing network is an abstract device built up of N wires, thought of as running from left to right, and M balancers that connect pairs of wires. The wires are numbered from 1 to N from top to bottom, and the balancers are numbered from 1 to M from left to right. Balancer i connects wires x_i and y_i (x_i < y_i).

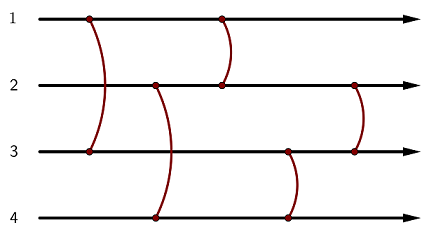
Each balancer must be in one of two states: up or down.

Consider a token that starts moving to the right along some wire at a point to the left of all balancers. During the process, the token passes through each balancer exactly once. Whenever the token encounters balancer i, the following happens:

• If the token is moving along wire x_i and balancer i is in the down state, the token moves down to wire y_i and continues moving to the right.
• If the token is moving along wire y_i and balancer i is in the up state, the token moves up to wire x_i and continues moving to the right.
• Otherwise, the token doesn't change the wire it's moving along.

Let a state of the balancing network be a string of length M, describing the states of all balancers. The i-th character is ^ if balancer i is in the up state, and v if balancer i is in the down state.

A state of the balancing network is called uniforming if a wire w exists such that, regardless of the starting wire, the token will always end up at wire w and run to infinity along it. Any other state is called non-uniforming.

You are given an integer T (1 \le T \le 2). Answer the following question:

• If T = 1, find any uniforming state of the network or determine that it doesn't exist.
• If T = 2, find any non-uniforming state of the network or determine that it doesn't exist.

Note that if you answer just one kind of questions correctly, you can get partial score.

Constraints

• 2 \leq N \leq 50000
• 1 \leq M \leq 100000
• 1 \leq T \leq 2
• 1 \leq x_i < y_i \leq N
• All input values are integers.

Partial Score

• 800 points will be awarded for passing the testset satisfying T = 1.
• 800 points will be awarded for passing the testset satisfying T = 2.

Sample Input 1

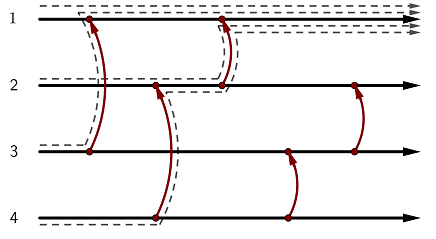
4 5 1
1 3
2 4
1 2
3 4
2 3

Sample Output 1

^^^^^

This state is uniforming: regardless of the starting wire, the token ends up at wire 1.

Sample Input 2

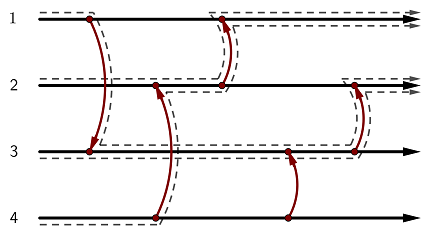
4 5 2
1 3
2 4
1 2
3 4
2 3

Sample Output 2

v^^^^

This state is non-uniforming: depending on the starting wire, the token might end up at wire 1 or wire 2.

Sample Input 3

3 1 1
1 2

Sample Output 3

-1

A uniforming state doesn't exist.

Sample Input 4

2 1 2
1 2

Sample Output 4

-1

A non-uniforming state doesn't exist.