競技プログラマーは日々最短経路問題を解いている。BFS や、ベルマンフォード、ダイクストラ、ワーシャルフロイドと多くのアルゴリズムも知られている。
あなたはそんな中、どうしても解けない最短路問題があった。それはグラフを見ずに最短路問題を解けという問題だ!こんなもの通常の人類には解けるわけがないのだが、30 分だけ ivvivvi 神の天啓を受けることができるようになった。
ivvivvi 神は競技プログラミングにも最短経路問題にも精通しており、どんなグラフに対しても任意の 2 点間の最短経路長を定数時間で求める能力を持っている。あなたは ivvivvi 神の力を借りて最短経路問題を解こうと思ったが、残念ながらあなたの解くべき最短経路問題では具体的な経路を出力しなければならない。ivvivvi 神なら、最短経路の復元も容易だが、ivvivvi 神は非常に忙しいので、これ以上手を煩わせるわけには行けない。そこで、できるだけ少ない質問回数で自力で最短経路を復元することにした。
3 つの整数 N、 s、そして、t が与えられる。このとき、頂点数 N のグラフがあり、頂点数以外の辺数や頂点の隣接関係などのグラフに関する情報は与えられないが、2 頂点 u、v の距離を質問することができる。ここで、グラフの頂点番号は 1 以上 N 以下である。5N 回以下の質問回数で s から t への最短路を発見し、最短路を表す頂点列を 1 つ出力せよ。
この問題では 2 頂点 u、v 間の距離をジャッジに質問しなければならない。 標準出力に次のように出力することで、u、v 間の距離を質問することができる。
? u v
このように標準出力したあと、この答えは標準入力に 1 行の整数として与えられる。 この問題ではプログラムの行った質問の回数が 5N 回を超えると誤答(WA)と判定される。この問題では最後に頂点列、つまり整数列を出力する。頂点列 (x_1, ..., x_k) を出力する出力形式は次のようである。
! x_1 x_2 ... x_k
ここで、出力は x_1 = s 、 x_k = t を満たし、任意の1 \leq i \leq k - 1 に対して、x_i と x_{i + 1} を直接結ぶ辺が存在する。 さらに、この最終的な解答は、一度しか行うことができない。この解答が正しい出力だったとき、正答とみなす。さらに、標準出力として上記の 2 つの記法と異なる出力や質問回数が 5N 回を超えた時はジャッジは -1 を返す。この時、即座にプログラムを終了させない場合、ジャッジが WA を正しく判定することを保証しない。
また、標準出力を行う毎に、ストリームをフラッシュ (flush) する必要があることに注意されよ。主要な言語でのフラッシュ例を以下に示す。もちろん、これ以外の方法でフラッシュを行っても構わない。
C 言語:
#include <stdio.h> fflush(stdout);
C++:
#include <iostream> std::cout.flush();
Java:
System.out.flush();
Python:
print(end='', flush=True)
入力として整数 3 つが与えられる。
N s t
| 標準入力 | 標準出力 |
|---|---|
| 4 1 3 | |
| ? 4 3 | |
| 3 | |
| ? 1 4 | |
| 2 | |
| ? 2 1 | |
| 1 | |
| ? 3 2 | |
| 2 | |
| ? 1 3 | |
| 3 | |
| ? 4 2 | |
| 1 | |
| ! 1 2 3 |
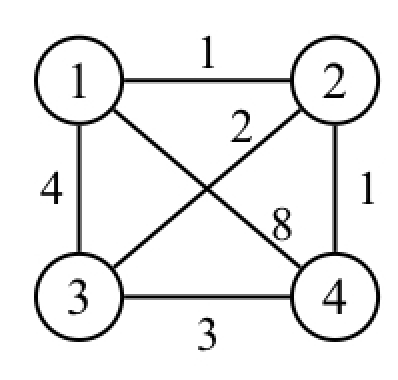
この入出力例では以下のグラフに対して 2 点間の距離を質問している。