Problem D: Course Planning for Lazy Students

会津大学では2009年度より、授業履修に関する新しい制度を開始した。新制度では必修科目を撤廃し、それぞれの進路を考慮して科目を自由に選択できるようになった。

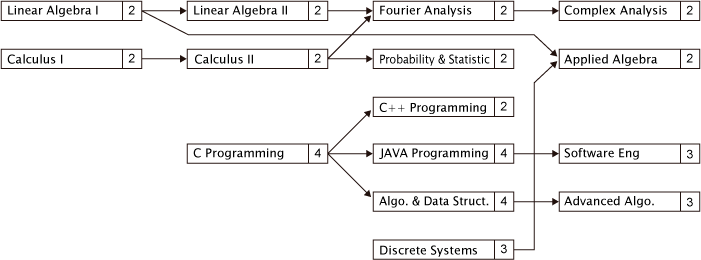
しかし、どの科目も無条件で履修できるわけではなく、特定の科目を履修するためには、先修条件を満たしている必要がある。下図に履修計画表の一部の例を示す：

図の長方形が１つの科目を表し科目名と単位数を含んでいる。図の矢印が先修条件を表す。矢印の意味は、矢印の終点で指されている科目を履修するためには、その矢印の始点を示す科目を修得している必要がある。例えば、Linear Algebra II (線形代数２)を履修するためには、Linear Algebra I (線形代数１)を修得している必要がある。また、Applied Algebra (応用代数)を履修するためには、Linear Algebra I と Discrete Systems (離散系論)の両方を修得している必要がある。

さて、履修登録計画において卒業に要する最低限の合計単位数 U を満たす履修科目の組み合わせは、怠慢な学生にとって興味深いものである。

あなたの仕事は、与えられた履修計画表と U を読み込み、最低限の履修科目数を報告するプログラムを作成することである。これは計画であるため、履修登録した科目は必ず単位を修得できるものと仮定する。

Input

入力は複数のデータセットからなる。各データセットは以下の形式で与えられる：

n U
c₀ k₀ r0₁ r0₂ ... r0_k0
c₁ k₁ r1₁ r1₂ ... r1_k1
.
.
c_n-1 k_n-1 r(n-1)₁ r(n-1)₂ ... r(n-1)_kn-1

n (1 ≤ n ≤ 20) は履修計画表が含む科目の数を示す整数である。科目には 0 から n-1 までの番号が割り当てられているものとし、以下 i 番目の科目を科目 i と呼ぶことにする。

U (1 ≤ U ≤ 100) は必要な合計単位数を表す整数である。

c_i (1 ≤ c_i ≤ 10)は科目 i の単位数を示す。次の k_i (0 ≤ k_i ≤ 5) は科目 i の先修科目の数を示す。それに続く ri₁ ri₂ ... ri_ki は科目 i の先修科目の科目番号を示す。

ある科目から先修条件を表す矢印を１つ以上たどり、再びその科目に戻るような入力は与えられない。また、U を満たす科目の組み合わせが必ず存在すると仮定してよい。

n と U がともに 0 のとき入力の終わりを示す。データセットの数は 100 を超えない。

Output

各データセットについて、最低限必要な科目数を１行に出力せよ。

Sample Input

4 4
1 0
3 2 0 2
2 0
2 0
3 6
1 0
3 2 0 2
2 0
0 0

Output for the Sample Input

2
3