素数の性質

4 で割ると 3 あまる素数 n (11、19、23 など) には、面白い性質があります。1 以上 n 未満の自然数 (1, 2,... , n - 1) を 2 乗したものを n で割ったあまりを計算した結果を並べると、同じ数になるものがあるため、互いに異なった数の個数は、(n - 1)/2 になります。

この様にして得られた数の集合には、特別な性質があります。得られた数の集合から、互いに異なる 2 つ a と b を選んでその差を計算します。差が負になったときは、その差に n を足します。さらに結果が (n - 1)/2 より大きいときは、その差を n から引きます。

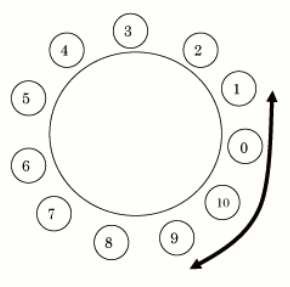
例えば、n = 11 のとき 1 と 9 の差は、1 − 9 = −8 → −8 + n = −8 + 11 = 3 になります。9 と 1 の差も 9 −1 = 8 → n − 8 = 11 − 8 = 3 で、同じ値 3 になります。この差は、円周上に 0, 1, ・・・, n - 1 を書いて、二つの数字の間の短い方の円弧を考えるとわかりやすくなります。(下図参照)

こうして得られた数の「差」は、1, 2, . . ., (n - 1)/2 のいずれかであり、同じ回数出現します。

【例】 n = 11 の時は、以下のようになります。

1. 1 から n-1 までの数を 2 乗したものを n で割った余りを計算します。

    12  =    1   →   1
    22  =    4   →   4
    32  =    9   →   9
    42  =   16   →   5
    52  =   25   →   3
    62  =   36   →   3
    72  =   49   →   5
    82  =   64   →   9
    92  =   81   →   4
   102  =  100   →   1
   

2. a, b の「差」の計算
   
   
   1. 1 で得られた 1, 3, 4, 5, 9 について異なる数同士の差を計算します。
   2. 計算結果が負の場合、n = 11 を加算します。
   3. さらに、計算結果が (n-1)/2 = 5 より大きい場合 n = 11 から減算します。
3. 出現回数を求める
   

   計算結果 1, 2, 3, 4, 5 の出現回数をそれぞれ数え上げます。

これらの計算結果から 1, 2, 3, 4, 5 の出現回数が 4 回であることがわかります。この性質は 4 で割ると 3 あまる素数特有の性質であり 4 で割ると 1 あまる素数ではこのようなことはおきません。このことを確認するため、10000 以下の奇数 n を入力とし、例題にあるような計算 (n で割ったあまりの 2 乗の差の頻度を求める)を実行し、その出現回数を出力するプログラムを作成してください。

Input

複数のデータセットが与えられます。各データセットとして１つの整数 n　(n ≤ 10000) が１行に与えられます。入力は 0 を１つ含む行でおわります。

Output

各データセットについて、出現頻度を以下の形式で出力してください。

剰余の平方の差が 1 である(a, b)の出現個数(整数)
剰余の平方の差が 2 である(a, b)の出現個数(整数)
   :
   :
剰余の平方の差が (n-1)/2 である(a, b)の出現個数(整数)

Sample Input

11
15
0

Output for the Sample Input

4
4
4
4
4
2
2
4
2
4
4
2